QUBIC BLOG POST
Neuraxon Time: Why Intelligence Is Not Computed in Steps, but in Time
Written by
Qubic Scientific Team
Published:
Jan 7, 2026
Listen to this blog post
The brain does not compute in time, rather it computes with time.
Biological neurons do not function like a bedroom light switch being turned on. They are a continuous dynamic system. The neuronal state evolves constantly, even in the absence of external stimuli.
How does a neuron function over time?
Basically, by moving electrical charges (ions) in or out of its membrane, that is, by changing its electrical potential. Ions enter or leave (mainly sodium and potassium) through the different gates of the neuron with a certain intensity, modifying the potential. There are some gates, called leakage gates, where ions are always entering and leaving.
Time is implicit. The electrical potential changes constantly, over time.
The change in a neuron’s electrical potential over time depends on:
The external current applied + the balance between the flows of sodium ions (which increase it) and potassium ions (which decrease it) through the gates that open and close.
Don’t panic with the graph. Positive and negative electrical charges (ions) flow through the gates causing depolarization (so current moves along to the end of the neuron) or hiperpolarization (so it comes back to a neutral state).
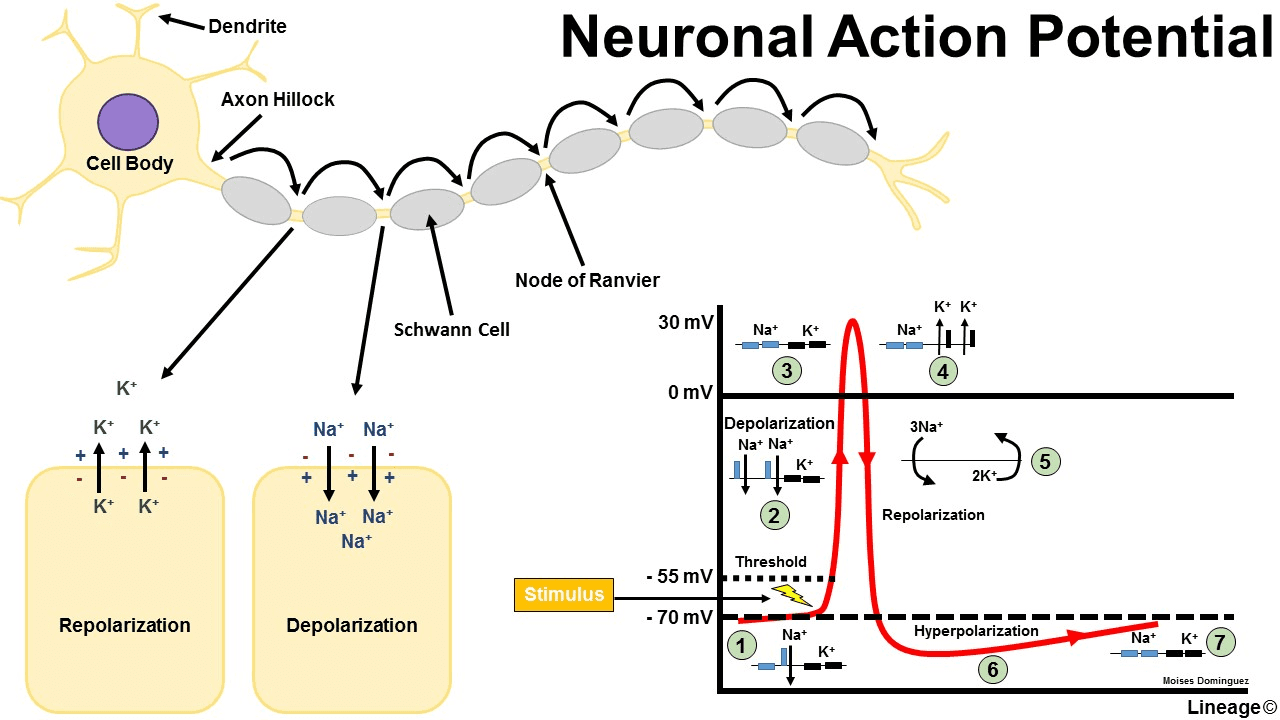
The potential (V) changes over time, that is mathematically, dV/dt, as a function of the sum of the input and output gates.
This is the fundamental model of computational neuroscience, which expresses that the state of the neuron depends both on current signals and on its immediate history. There is no “reset” between events, since each stimulus falls onto a system that is always running.
Now let’s move to Neuraxon, which is a bio-inspired model.
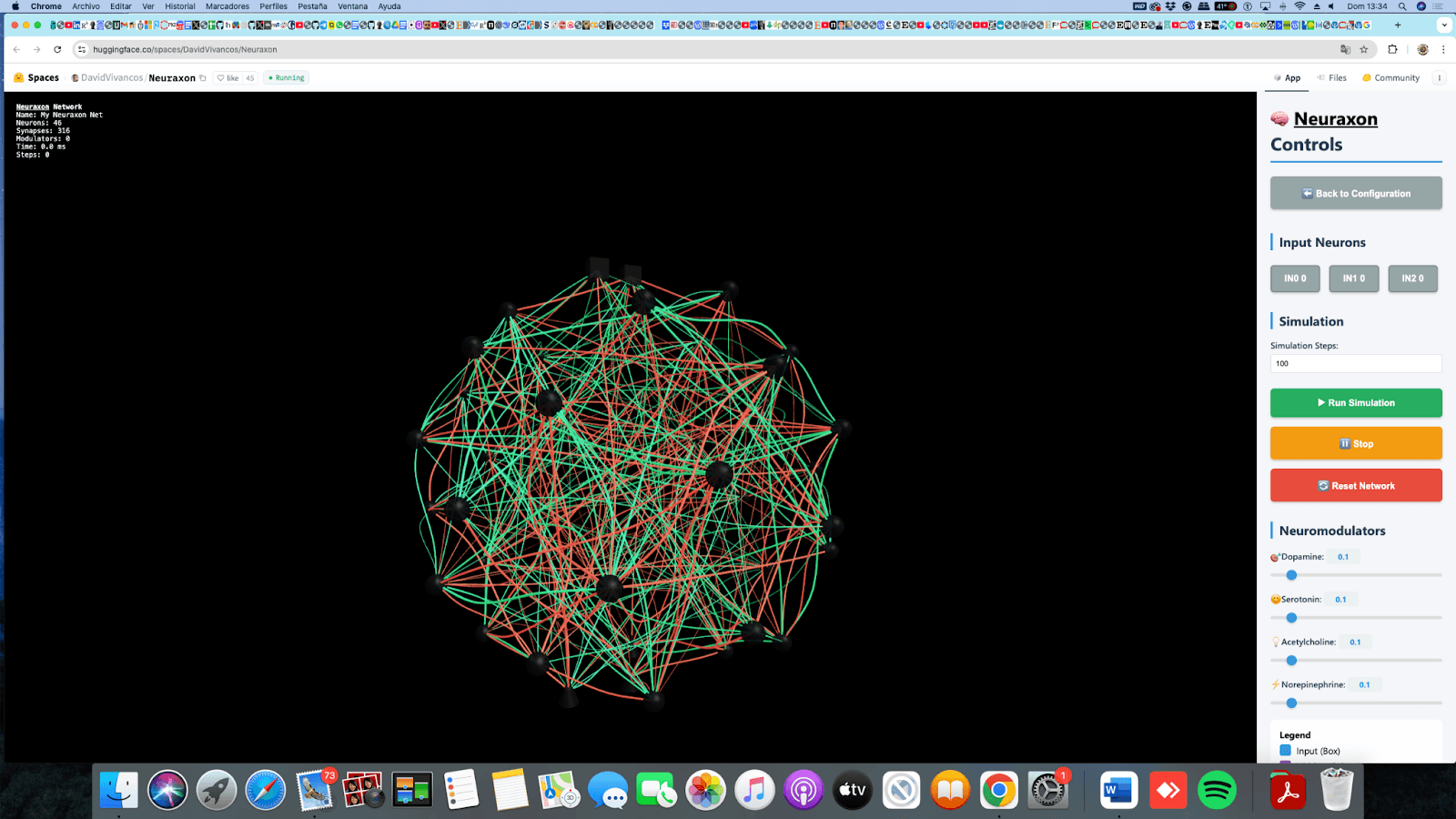
We want it to be alive, an intelligent tissue. It cannot have discrete states, but continuous ones.
In Neuraxon, instead of ion gates that open and close and move charges with a certain intensity, changing voltage, we have dynamic synaptic weights. But the model equation maintains a clear and direct similarity with the biological neuron.
What does this mean?
Instead of V, voltage in biological neuron, the state of Neuraxon, is s. And it changes over time too, therefore ds/dt is a function of the weights and activations and the previous state.
Unlike a classical AI model, where the synaptic weights of a network represent stereotyped outputs to an input, in Neuraxon the weights are not static.
Imagine, for example, an “email inbox” automatic response mechanism.
In classical AI, the rule does not adjust or change over time or context.
In Neuraxon, it is taken into account whether the “email input” comes from the same person (which could indicate urgency) or whether it arrives on a weekend (which may generate a no-response output). In other words, the rule remains, but when and how the response is given is modulated.
Do LLMs compute time?
Large language models appear to show deep understanding in many contexts, but they operate under a logic different from biological systems (Vaswany, 2017). They do not function based on an internal temporal dynamic, on a “change in potential” or on “synaptic weights” that modulate response, but rather process discrete sequences.
In LLMs, “time” does not exist, which makes it difficult for them to simulate biological behavior (such as intelligence). LLMs know how to distinguish which word comes before and which comes after, but they do not grant an experience of duration or persistence. Order replaces time.
Unlike Neuraxon, they do not possess internal rhythms that speed up or slow down, nor do they show progressive habituation to repeated stimuli, nor can they dynamically anticipate based on an internal state that changes over time.
The LLM model computation would be something like:
output = Fθ(input)
so outcomes are fixed solutions from a function (combination) of inputs.
There is no state as a function of time. These are data that form huge matrices and change their value through a specific function, which, as in the example cited, restricts the possibilities: email input → automatic response.
Wrapping up. The distance between bio-inspired models such as Neuraxon and large language models should not be explained in terms of computational power or data volume. There is a deeper difference.
The brain is, in itself, a continuous temporal system. Its functioning is defined by dynamics that unfold over time, by states that evolve, decay, and reorganize permanently, even in the absence of external stimuli (Deco et al., 2009; Northoff, 2018).
Neuraxon deliberately positions itself within that same logic. It does not attempt to imitate 1 to 1 the biophysical complexity of the brain, but it explicitly incorporates time as a computational variable. Its internal state evolves continuously, carries the past, and modulates the present, allowing adaptation without the need for a reset.
LLMs, by contrast, operate very differently. They manipulate symbols ordered in discrete sequences without their own temporal dynamics. There is no time, only order. There is no adaptation, only pre-defined responses.
As long as time does not form part of the state governing computation, LLMs may be effective, but they will hardly be autonomous in a strong sense.
Future artificial intelligence aims to operate in dynamic environments. This is the reason why Neuraxon includes time as a fundamental variable.
A living intelligence tissue…
How This Relates back to Qubic?
Qubic provides the continuously running, stateful computational environment required for time-aware intelligence.
It is the natural substrate on which models like Neuraxon - adaptive, persistent, and never “resetting” - can exist and evolve.
Addenda
Take a look at the equations. Don´t panic!
1 Biological neuron, V potencial, “sum of gates flux in & out”
2 Neuraxon model equation - clear and direct similarity with the biological neuron.
s state, wi & f(si) dynamic synaptic weights
3 LLM model equation. Inputs (ordered in a matrix) create matrix outputs through a fixed function
p (xn+1 | x₁, …, xn) = softmax (Fθ (x₁, …, xn) )
References